This paper is in the proceedings of the 1997 Workshop on Languages and Compilers for Parallel Computing (LCPC97).
H. G. Dietz, T. I. Mattox, and G. Krishnamurthy
School of Electrical and Computer Engineering
Purdue University
West Lafayette, IN 47907-1285
{hankd,
tmattox,
gayathri}@ecn.purdue.edu
http://garage.ecn.purdue.edu/~papers/
The concept of "data parallelism" is a pervasive force throughout parallel processing. Although a certain level of processing-element autonomy can help performance, the fact is that many parallel algorithms, applications, and compiler analysis techniques focus on identifying a set of data objects that can be processed using loosely synchronous parallelism. Thus, it is not surprising that a large number of communication libraries support at least a few synchronized aggregate operations on data. Over the past few years, we have developed eleven different types of PAPERS (Purdue's Adapter for Parallel Execution and Rapid Synchronization) hardware specifically to efficiently implement aggregate functions for clusters of PCs or workstations.
The Aggregate Function Application Program Interface (AFAPI) library was initially designed to be a portable high-level interface to the various types of PAPERS cluster hardware, so one would expect it to work well using this custom hardware, and it does work well. In this paper, we show that the AFAPI is also an efficient programming model for other types of parallel systems -- especially shared memory multiprocessors. For many operations, AFAPI can outperform threads libraries and other more traditional shared memory programming models.
To aid navigation within this document, a Hypertext Index is included at the end of this document (click here to jump to the Hypertext Index).
In any discussion of programming models for parallel computers, one of the first topics to arise is inevitably the choice between shared memory and message passing communication. Advocates of shared memory communication see programs as consisting of shared data structures augmented by a multitude of synchronization mechanisms that can be used to control parallel access to these structures. In contrast, message passing enthusiasts see each processor as fundamentally independent, working on its own data until it is necessary to inform another processor of what has been done.
The AFAPI represents a third, fundamentally different, model for interactions between processors. Each AFAPI operation is an aggregate operation, requested and performed in unison by all processors. Thus, although the AFAPI routines can be called from MIMD or SIMD-style code, all AFAPI operations are based on a model of aggregate interaction that closely resembles SIMD communication. This is not a coincidence; years of research involving Purdue University's PASM (PArtitionable Simd Mimd) prototype supercomputer experimentally demonstrated that SIMD-like interactions are more efficient than asynchronous schemes for a wide range of applications [1]. The problem was that systems like PASM and PAPERS [7] clusters use custom hardware to efficiently implement aggregate operations.
Clearly, just as shared-memory hardware can simulate message passing and message-passing hardware can simulate a shared memory, either type of hardware can simulate the aggregate functions of the AFAPI. The surprise is that such simulations can be efficient enough to compete with the native execution models. This is accomplished by implementing the library using methods that allow the simulation to take advantage of the same aggregate function properties that make the PAPERS hardware so simple and efficient.
To date, versions of the AFAPI have been implemented for:
Porting programs that use the AFAPI between these platforms is literally a matter of recompiling using the appropriate version of the library. Although there are significant differences in the overall speed of the different versions (e.g., UDPAPERS AFAPI tends to be much slower than SHMAPERS AFAPI), the relative timing of operations within each version of the AFAPI does not vary as widely; thus, the selection of which AFAPI routines to use can be somewhat optimized without knowing which library version will be used.
Section 2 provides an overview of the complete AFAPI, including measured execution times for a sampling of the aggregate functions on a variety of cluster and shared memory multiprocessor platforms. The surprisingly good efficiency of the SHMAPERS AFAPI is due to a lock-free aggregate function implementation; the implementation of SHMAPERS AFAPI is described in Section 3. This section also compares the performance of the SHMAPERS AFAPI implementation to that of a more conventional threads-based approach. In conclusion, Section 4 briefly summarizes the contributions of this work and the primary directions for future work.
Once upon a time (1994, actually), there was the PAPERS library [3]. It was good, but it only worked with either a real TTL_PAPERS unit or a "virtual" TTL_VAPERS simulator. This simulator used multiple UNIX processes communicating through pipes, and was accurate to the level of bit patterns sent through the simulated ports, even using X windows to display an image of the TTL_PAPERS wooden front panel complete with flashing lights. Unfortunately, that simulator was also very slow, and people told us that was bad... because they didn't have PAPERS hardware and didn't want to run at simulated speeds. At the same time, we realized that higher-performance versions of PAPERS will vary in precisely what functions are implemented directly in hardware; it was time to standardize the user interface to ensure user code portability.
Thus was born AFAPI (pronounced "ah-fa'-pea"), a fully abstract program interface that seeks to provide the most important aggregate communication functions in as clean and portable a structure as possible. AFAPI has numerous improvements over the old libraries, including more consistent naming conventions and the addition of an aggregate signal system. It is designed to provide a very simple, intuitive, yet complete, parallel programming model suitable both for direct use by programmers and as the target of optimizing compilers.
The following subsections overview the AFAPI programming model, also giving benchmark times for representative AFAPI functions on a variety of platforms. Other papers have demonstrated the scalability of TTL_PAPERS hardware and how to build higher-performance PAPERS units [7]; we have built PAPERS clusters with up to 24 machines, and the PAPERS 960801 modules can connect thousands without modification. Our concern in this paper is primarily showing that, for the range of number of processors found in the most cost- effective shared memory machines, SHMAPERS AFAPI is more than competitive with TTL_PAPERS AFAPI. Toward this goal, the benchmark AFAPI versions and system configurations are:
The exact same 90 MHz Pentium systems were used for all the cluster benchmarks, and the dual-processor 100 MHz Pentium system is as close a match to these systems as we had available. All the 248 MHz SPARC V9 benchmarks were done using the same machine. Shared memory machines are generally more sensitive to OS scheduler activity than are clusters, so the benchmark times reported for all systems are "wall clock" times; these times include OS scheduler interference from a variety of typically inactive processes, including an X windows server. All times are given in microseconds (µs).
Because the AFAPI communication model is based on n-way interaction between processors (as opposed to memory block transfers), most routines have a version for each processor- or language-distinguished data type. The data types supported, their portable AFAPI type suffixes, and the operation classes supporting these types, are given in the following table:
+-----------------------------+--------+---------------------------+ |GCC Type | Suffix | Classes | +-----------------------------+--------+---------------------------+ |int (barrier group bit mask) | bar | alpha, beta | |int (boolean) | 1u | alpha, beta, delta, gamma | |char | 8 | alpha, beta, delta, gamma | |unsigned char | 8u | alpha, beta, delta, gamma | |short | 16 | alpha, beta, delta, gamma | |unsigned short | 16u | alpha, beta, delta, gamma | |int | 32 | alpha, beta, delta, gamma | |unsigned int | 32u | alpha, beta, delta, gamma | |long long | 64 | alpha, beta, delta, gamma | |unsigned long long | 64u | alpha, beta, delta, gamma | |float | 32f | alpha, gamma | |double | 64f | alpha, gamma | |void * | ptr | alpha, beta | |(byte block, compressed) | z | z | +-----------------------------+--------+---------------------------+
Because the size of each standard C data type can vary across machines, AFAPI portable type names are constructed by placing p_ in front of the suffix; e.g., unsigned int is p_32u, double is p_64f, and char is p_8. The names of the various library operations are similarly constructed using the appropriate type suffix. Because some operations only make sense for certain data types (e.g., bitwise operations do not make sense relative to a p_32f), the class meta- symbols are used in this paper to indicate which suffixes are supported; for example, the valid AFAPI type names could be described as p_alpha.
There are three predefined names used by nearly all AFAPI programs. The compile-time integer constant NPROC is the number of processors available in the system; it is fixed in the library as a compile-time constant so that it can be used in declaring the dimensions of static arrays. The number of this processor, in the range 0..NPROC-1, is given by (const int) IPROC. The last predefined name is (const int) CPROC, which gives the processor number of console/control process -- the one process that is connected to the UNIX standard stdin, stdout, and stderr; having only a single process connected in this way is more compatible with UNIX file I/O conventions. By default, CPROC is typically 0, although it can be any processor in the range 0..NPROC-1.
There are only three basic functions used to control the aggregate function communication system. The int p_init(void) function is used by each process to check-in with the AFAPI; it returns 0 if successful. The routine used to check-out is void p_exit(void). The third routine is used solely in support of fault tolerance; int p_confirm(void) returns 0 if the AFAPI has performed all operations correctly since the last check, and otherwise attempts to recover and returns a non-zero error code. Thus, int p_confirm(void) would be used just before committing to critical database changes, etc.
The simplest aggregate function, literally the aggregate "null operation," is barrier synchronization. A barrier is simply a parallel operation that does not complete until all processors have initiated the operation; thus, each processor waits until all processors have arrived at the barrier, and then all processors simultaneously resume executing. Using AFAPI, this is done either by calling the function void p_wait(void) or by using the inline routine void p__wait(void) -- the inline version is provided because the function call overhead can be significant compared to the time taken for the barrier itself. Because AFAPI operations generally occur as side-effects of barrier synchronizations, a bad implementation of barriers would limit performance of nearly the entire library.
The simplest aggregate functions that involve data all have the property that, as a side-effect of barrier synchronization, they each examine a single data bit from each processor and yield either a single-bit answer or a result with single bit per participating processor. For each processor to compute a bit mask in which the bit with value 2k is set iff processor k's value for f!=0, every processor would call the function p_bar p_waitbar(p_1u f). If we only need to know if any processor had a value of f!=0, all processors instead call p_1u p_any(p_1u f). Similarly, to determine if all processors had values of f!=0, all processors would call p_1u p_all(p_1u f).
++-----------------++-------++------------------------------+
|| TTL_PAPERS ||CAPERS || SHMAPERS |
||2xP 3xP 4xP || 2xP ||2xP 2xS 3xS 4xS 5xS |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
|p__wait() ||3.8 | 3.8 | 3.8 || 11 ||0.65 | 0.87 | 1.7 | 2.4 | 3.1 |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
|p__waitbar(f) ||9.5 | 9.6 | 9.7 || 14 ||0.99 | 0.95 | 1.9 | 2.8 | 3.3 |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
|p__any(f) ||9.5 | 9.6 | 9.7 || 14 ||0.95 | 0.91 | 2 | 2.7 | 3.1 |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
|p__all(f) ||9.5 | 9.6 | 9.7 || 14 ||0.87 | 1 | 1.8 | 2.5 | 3.3 |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
|p_wait() ||4 | 4 | 4.1 || 11 ||0.73 | 0.94 | 1.8 | 2.4 | 3.2 |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
|p_waitbar(f) ||9.7 | 9.9 | 10 || 14 ||1.3 | 1 | 1.9 | 2.8 | 3.4 |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
|p_any(f) ||9.5 | 9.5 | 9.5 || 14 ||1.2 | 0.97 | 2 | 2.6 | 3.2 |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
|p_all(f) ||9.5 | 9.5 | 9.5 || 14 ||1.1 | 1 | 1.9 | 2.6 | 3.5 |
+--------------++----+-----+------++-------++-----+------+-----+-----+-----+
The above table lists measured performance of the AFAPI primitives. In viewing this table (and the other tables in this paper), it is important to note that these times are fast compared to most supercomputers and other methods. For example, the Cray T3D [2] can execute a 4-processor p__wait() in 1.7µs (or about 21µs under PVM); 4 processors of an Intel Paragon XP/S [8] take about 530µs for the same operation. Minimum time for a single message on an IBM SP1 [5] is around 30µs. Even a simple ping operation within a typical machine takes about 300µs; software barriers using UNIX sockets cannot exceed that speed and typical PVM and MPI cluster performance is much worse.
Although aggregate functions can do more than passive communication, they can also efficiently implement a variety of communication functions.
A very simple aggregate communication is broadcast. Unlike most aggregate functions, broadcast is asymmetric in that the sole sender must execute a function which is different from that executed by the receivers: the sender calls void p_bcastPutalpha(p_alpha d) to output its value of d, while the receivers all call p_alpha p_bcastGetalpha(void) to get the value sent. There is also a version of these calls to broadcast a block of n bytes from/into address a using compression; the sender calls void p_bcastPutz(void* a, int n) and the receiver calls void p_bcastGetz(void* a, int n).
Although broadcast is an obvious aggregate communication, the most fundamental aggregate communication is p_alpha p_putGetalpha(p_alpha d, int s), which implements an arbitrary multibroadcast without interference. Unlike message passing and shared memory models in which the sender supplies both the data and the destination address, in this operation the sender simply provides the data object d, and the receiver selects which sender, s, it wants the data from. Of course, as an aggregate operation, every processor is simultaneously both a sender and a receiver. The efficiency of this operation lies in the fact that multiple readers of one processor's data do not cause contention nor is the sender required to list all receivers of its data.
Additionally, the AFAPI provides scatter and gather operations that collect or spread arrays of data across all processors. To gather an array such that p[i] = d from processor i, all processors call void p_gatheralpha(p_alpha *p, p_alpha d). In contrast, scatter has the same asymmetry as broadcast; for processor i to get p[i] from the sender, the sender calls p_alpha p_scatPutalpha(p_alpha *p) and the receiver calls p_alpha p_scatGetalpha(void).
++----------------++-------++------------------------------+
|| TTL_PAPERS ||CAPERS || SHMAPERS |
||2xP 3xP 4xP || 2xP ||2xP 2xS 3xS 4xS 5xS |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
|p_bcastPut8(d)/ || 19 | 20 | 21 || 25 ||0.97 | 1.3 | 2.2 | 2.8 | 3.6 |
|p_bcastGet8(d) || | | || || | | | | |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
|p_bcastPut16(d)/ || 51 | 52 | 55 || 63 ||0.98 | 1.3 | 2 | 2.8 | 3.6 |
|p_bcastGet16(d) || | | || || | | | | |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
|p_bcastPut32(d)/ || 92 | 95 | 99 || 112 ||0.91 | 1.3 | 2.1 | 2.7 | 3.6 |
|p_bcastGet32(d) || | | || || | | | | |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
|p_bcastPut64(d)/ ||102 | 106 | 110 || 126 ||1 | 1.3 | 2.2 | 2.8 | 3.6 |
|p_bcastGet64(d) || | | || || | | | | |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
|p_putGet8(d,s) || 34 | 51 | 55 || 28 ||1.1 | 0.96 | 1.7 | 2.7 | 3.2 |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
|p_putGet16(d,s) || 60 | 115 | 120 || 56 ||1.2 | 0.96 | 1.7 | 2.5 | 3.2 |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
|p_putGet32(d,s) ||101 | 202 | 211 || 113 ||1.1 | 0.96 | 1.7 | 2.5 | 3.2 |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
|p_putGet64(d,s) ||112 | 223 | 232 || 228 ||1.3 | 0.97 | 1.8 | 2.5 | 3.2 |
+-----------------++----+-----+-----++-------++-----+------+-----+-----+-----+
An associative reduction is an aggregate function in which all processors are given the result which is obtained by applying the specified associative (operand order- insensitive) operation to the data values output by all processors. There are bitwise reductions for Ops of And, Or, and Xor (exclusive OR); these are all of the form p_beta p_reduceOpbeta(p_beta d). There are also comparative reductions Min (minimum value) and Max (maximum value), with the form p_alpha p_reduceOpalpha(p_alpha d). Finally, if working with integers or ignoring potential floating point overflow, underflow, and precision variations, Add and Mul can be used for associative reduction operations of the form p_gamma p_reduceOpgamma(p_gamma d).
++----------------++-------++-----------------------------+
|| TTL_PAPERS ||CAPERS || SHMAPERS |
||2xP 3xP 4xP || 2xP ||2xP 2xS 3xS 4xS 5xS |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceOr8(d) || 19 | 19 | 20 || 28 ||1.3 | 1 | 2.1 | 2.8 | 3.7 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceOr16(d) || 38 | 38 | 38 || 55 ||1.2 | 1 | 1.9 | 2.8 | 3.7 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceOr32(d) || 76 | 76 | 77 || 112 ||1.1 | 0.99 | 1.9 | 2.6 | 3.8 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceAdd8(d) || 38 | 62 | 81 || 28 ||1.3 | 1.1 | 2 | 2.8 | 3.6 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceAdd16(d) || 99 | 158 | 219 || 55 ||1.3 | 1 | 2 | 2.7 | 3.9 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceAdd32(d) ||184 | 288 | 399 || 112 ||1.2 | 0.99 | 2.1 | 2.7 | 3.8 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceMul8(d) || 39 | 62 | 80 || 28 ||1.3 | 1.2 | 2.2 | 3 | 3.9 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceMul16(d) ||100 | 157 | 219 || 55 ||1.4 | 1.2 | 2.3 | 3.1 | 3.9 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_reduceMul32(d) ||184 | 286 | 401 || 112 ||1.4 | 1.4 | 2.5 | 3.1 | 3.9 |
+-----------------++----+-----+-----++-------++----+------+-----+-----+-----+
Scans, also known as parallel prefix operations, are closely related to associative reductions. However, whereas a reduction returns the same value to all processors, a scan returns to each processor i the value of a reduction across only processors 0..i. The same operations supported as reductions are also supported as scans; the function calls differ only in that scan is substituted for reduce in the function name, e.g., scan And is p_beta p_scanAndbeta(p_beta d).
++----------------++-------++-----------------------------+
|| TTL_PAPERS ||CAPERS || SHMAPERS |
||2xP 3xP 4xP || 2xP ||2xP 2xS 3xS 4xS 5xS |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanOr8(d) ||20 | 41 | 40 || 25 ||1.2 | 1 | 1.9 | 2.6 | 3.2 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanOr16(d) ||51 | 105 | 144 || 63 ||1.3 | 1 | 1.9 | 2.5 | 3.2 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanOr32(d) ||95 | 190 | 299 || 112 ||1.2 | 0.97 | 1.9 | 2.5 | 3.2 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanAdd8(d) ||21 | 41 | 65 || 25 ||1.2 | 1 | 1.9 | 2.5 | 3.2 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanAdd16(d) ||51 | 105 | 164 || 63 ||1.3 | 1 | 1.9 | 2.6 | 3.2 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanAdd32(d) ||93 | 190 | 297 || 112 ||1.2 | 0.99 | 1.9 | 2.5 | 3.2 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanMul8(d) ||20 | 43 | 65 || 25 ||1.5 | 1.2 | 2.1 | 2.7 | 3.3 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanMul16(d) ||52 | 105 | 164 || 63 ||1.5 | 1.2 | 2.1 | 2.5 | 3.4 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
|p_scanMul32(d) ||94 | 191 | 299 || 113 ||1.3 | 1.2 | 2.1 | 2.6 | 3.4 |
+---------------++----+-----+-----++-------++----+------+-----+-----+-----+
Although the above operations are becoming common additions to message passing libraries like PVM [6] and MPI [9], there are a number of more obscure aggregate functions that are just as important. These functions are rarely used to transmit data, but rather to determine characteristics of the global state of the parallel computation toward implementing more efficient control, scheduling, or load balancing of the computation.
The int p_first(p_1u f) operation returns the IPROC of the lowest-numbered processor in which f!=0, and returns NPROC if no PE had f!=0. Similarly, it can be very useful to determine the number of processors for which f!=0, and this is done by int p_count(p_1u f). In fact, often one does not need a precise count, but just an approximate number; int p_quantify(p_1u f) returns 0 if no processor has f!=0, 1 if just one does, 2 (or more) if at least 2 processors have f!=0, and NPROC if all processors have f!=0.
For scheduling access to shared resources, AFAPI provides four basic operations. Voting operations allow each processor to vote for the processor that it wants to interact with; int p_voteCount(int v) returns the number of processors that voted for processor IPROC, while p_bar p_vote(int v) returns a bit vector with 2k set iff processor k voted for v==IPROC. Matching operations are similar, but collect votes based on which processors voted for the same value that this processor voted for; int p_matchCountbeta(p_beta v) returns the number of processors that voted for the same value this processor voted for, and p_bar p_matchbeta(p_beta v) returns a bit vector with 2k set iff processor k voted for the same value.
Finally, it is common that an application will require data to be in a sorted order across the processors. For this purpose, int p_rankalpha(p_alpha d) returns the position that this processor's d would hold if the values from all processors were sorted into ascending order.
++----------------++-------++----------------------------+
|| TTL_PAPERS ||CAPERS || SHMAPERS |
||2xP 3xP 4xP || 2xP ||2xP 2xS 3xS 4xS 5xS |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_first(f) || 10 | 10 | 10 || 14 ||1.3 | 1 | 1.9 | 2.5 | 3.1 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_count(f) || 10 | 10 | 10 || 14 ||1.2 | 1 | 2 | 2.6 | 3.8 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_quantify(f) || 10 | 10 | 10 || 14 ||1.2 | 1 | 2.1 | 2.6 | 3.8 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_voteCount(s) || 18 | 29 | 39 || 14 ||1.2 | 1 | 2.3 | 2.8 | 3.5 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_vote(s) || 20 | 30 | 30 || 14 ||1.4 | 1.1 | 2.1 | 2.9 | 3.5 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_matchCount8(d) || 38 | 62 | 82 || 28 ||1.3 | 1.1 | 2.3 | 3 | 3.6 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_matchCount16(d) ||101 | 156 | 216 || 56 ||1.3 | 1.1 | 2.3 | 2.9 | 3.4 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_matchCount32(d) ||184 | 288 | 403 || 112 ||1.2 | 1 | 1.9 | 2.9 | 3.6 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_match8(d) || 38 | 62 | 81 || 28 ||1.4 | 1.1 | 2.2 | 2.8 | 3.5 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_match16(d) ||102 | 157 | 218 || 55 ||1.5 | 1.1 | 2.3 | 2.8 | 3.6 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_match32(d) ||184 | 288 | 401 || 112 ||1.4 | 1.1 | 1.9 | 2.7 | 3.5 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_rank8(d) || 38 | 62 | 81 || 28 ||1.4 | 1.1 | 1.9 | 2.7 | 3.3 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_rank16(d) ||100 | 157 | 218 || 56 ||1.4 | 1.2 | 1.9 | 2.7 | 3.4 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
|p_rank32(d) ||186 | 287 | 401 || 112 ||1.4 | 1.1 | 1.9 | 2.6 | 3.4 |
+------------------++----+-----+-----++-------++----+-----+-----+-----+-----+
In addition to the fully synchronous p_ routines described above, AFAPI provides a variety of s_ functions that implement a powerful asynchronous signal mechanism allowing any processor to signal all processors. This system supports arbitrary user-installed signal handlers as well as fully coherent, polyatomic, replicated shared memory [4].
The int s_init(void) enables the aggregate signal system, and void s_exit(void) disables it. int s_install(int s, void (*f)(p_bar m)) installs a user signal handler f() and returns the signal number it was assigned; void s_ignore(p_bar m) is the default handler. The function void s_signal(int s) is used to send the aggregate signal s, which will not be processed until all processors have called some s_ routine. The null operation s_ routine is void s_poll(void), which simply polls for pending signals; having signals generate interrupts would be too slow. To barrier synchronize, simultaneously ensuring that all previously- enqueued signals are first flushed, the library provides the void s_wait(void) call.
There is only one pre-installed signal handler, which manages replicated shared memory stores. You might be wondering why a SHMAPERS AFAPI user would use simulated shared memory when they have the real thing, but the AFAPI version offers object access semantics that would require careful use of locks if the hardware mechanism were used directly -- besides, AFAPI shared memory works with the same semantics on any hardware supported by AFAPI. The routine void s_update(void *a, int n) performs an atomic store of the n-byte object at logical address a, coherently updating the copies in all processors. In the worst case, all processors are storing into different objects simultaneously, yielding the performance listed for d arguments in the following table. If processors are storing into overlapping addresses (i.e., a write-write race), the performance is better, as shown by the s-argument entries. The void s_acquire(s_lock *l) and void s_release(s_lock *l) routines implement shared memory locks -- which the atomicity and race handling allow to be implemented literally as a single s_update(l, 1). Reads of shared objects are always fully coherent and local, with no overhead beyond that of local memory access.
++----------------------++-------++---------------------------------+
|| TTL_PAPERS ||CAPERS || SHMAPERS |
|| 2xP 3xP 4xP || 2xP ||2xP 2xS 3xS 4xS 5xS |
+--------------++------+-------+-------++-------++-----+------+------+------+------+
|s_poll() || 1.9 | 1.9 | 1.9 || 1.9 || 0.4 | 0.1 | 0.2 | 0.2 | 0.3 |
+--------------++------+-------+-------++-------++-----+------+------+------+------+
|s_wait() || 12 | 12 | 12 || 23 || 3.9 | 3.2 | 4.8 | 6.2 | 7.9 |
+--------------++------+-------+-------++-------++-----+------+------+------+------+
|s_update(s,1) || 76 | 88 | 103 ||115 || 9.9 | 9 | 15 | 22 | 31 |
+--------------++------+-------+-------++-------++-----+------+------+------+------+
|s_update(s,4) || 66 | 77 | 93 ||105 ||10 | 9.1 | 15 | 22 | 31 |
+--------------++------+-------+-------++-------++-----+------+------+------+------+
|s_update(d,1) ||150 | 217 | 290 ||205 ||12 | 12 | 23 | 39 | 60 |
+--------------++------+-------+-------++-------++-----+------+------+------+------+
|s_update(d,4) ||129 | 186 | 250 ||180 ||14 | 12 | 23 | 39 | 61 |
+--------------++------+-------+-------++-------++-----+------+------+------+------+
Not only is a barrier synchronization mechanism needed to implement void p_wait(void), but barrier synchronization is also required as a component of nearly all AFAPI operations. Without an efficient barrier implementation, AFAPI is not effective. The following three subsections briefly describe the implementation of barriers, the implementation of aggregate functions involving data communication, and a few words about virtual processors.
Although most shared memory multiprocessors do not directly implement barrier synchronization, techniques for implementing barriers using shared memory mechanisms have been widely studied. There are many ways to barrier synchronize using shared memory, including the use of various atomic operations. The most common approach uses atomic locking instructions to access a single shared counter. However, atomic operations and spin locks can truly swamp the bus or cache coherence logic.
One barrier implementation is given by Sun using their threads library, http://www.sun.com/workshop/sig/threads/share- code/Barrier/barrier.c.txt. On the same hardware, Sun's routine takes about 340µs to perform the equivalent of our 1.8µs SHMAPERS AFAPI 4xS p_wait(). However, there are a number of simple improvements that can be made to bring the locked-counter-based threads approach closer to the performance of our routine.
The lowest-level synchronization operation supported by Sun threads is mutex_lock(). To perform a barrier synchronization, each thread obtains the lock, decrements the counter, releases the lock, and then spin-waits for the counter to reach zero. The counter must be initialized to NPROC prior to the previous barrier, but this requires that the previous barrier use a different counter. Similarly, the counter used in the current barrier cannot be reset to NPROC until it can be guaranteed that every thread has observed the counter reaching zero, which results in an array of three barrier counters, with accesses to them sequenced in a round-robin fashion. The code is approximately:
mutex_t b_lock[3];
volatile int b_count[3];
int b_index[NPROC];
void t_wait(register int IPROC)
{
register int cur = b_index[IPROC];
register int next = (b_index[IPROC] = ((cur + 1) % 3));
b_count[next] = NPROC;
mutex_lock(&(b_lock[cur]));
--(b_count[cur]);
mutex_unlock(&(b_lock[cur]));
do { } while (b_count[cur]);
}
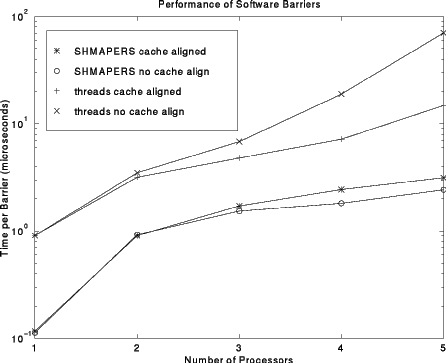
Although the code looks more complex, we also implemented a version that aligned the locks so that they would be in different cache lines. That brings the 4xS time down to about 7µs, which is still about four times slower than the AFAPI routine! The result of benchmarking the SHMAPERS AFAPI technique and both of the improved threads-based routines is summarized in the following figure (note that the times are plotted on a log scale).

Why are the SHMAPERS AFAPI versions so fast? Our approach uses no atomic locks. In fact, it is pure, highly portable, C code with UNIX System V shared memory segments shared by ordinary UNIX processes -- there are no special instructions nor operating system calls of any kind. The trick used is to give each processor its own separate counter, and to use a memory layout that ensures each counter is in a different cache line (to avoid "false sharing"). Because each counter is written by only a single processor, there is no need for an atomic lock; an ordinary load and volatile store will yield the same semantics as an atomic increment instruction would.
But how are these counters used? The answer is simply that if each processor increments its counter for every barrier, then a barrier is achieved when all counters have the same value. Reading the counters from all processors requires each processor to execute at least NPROC load operations, and perhaps many more if the processor has to spin reading a counter whose value has not yet been incremented. However, this spinning can be done using an ordinary load instruction, which will result in virtually all these reads being satisfied from cache. In fact, only the other processor incrementing its counter will cause the spinning processor to experience a cache miss, but this coherence traffic is then carrying the critical information that another processor is at the barrier.
Although use of NPROC counters solves several problems, as described above, it still has the problem of each processor not knowing when all other processors have recognized that the barrier is complete. This problem could be solved by, rather than comparing counters for equality, comparing every other processor's counter value for greater than or equal to this processor's value... however, this would then create the problem of how to handle the eventuality of the counters wrapping-around to smaller values. Our solution is simply to compare for equality with either the value of this processor's counter or one added to that value (which may be a smaller numeric value due to wrap-around); if each processor's counter value matches one or the other value, the barrier is complete.
From this logic, we are able to make yet another optimization: if some processor's counter value is equal to one plus our value, then that processor is waiting at the next barrier. If some processor is waiting at the next barrier, it logically follows that it must have detected that all the processors had reached the current barrier. Thus, upon detecting that any processor is at the next barrier, we immediately know that the current barrier has completed -- without actually examining every processor's counter. The code is:
extern inline void p__wait(void)
{
register volatile p_shm_type *p = p_shm_all;
register volatile p_shm_type *q = (p + NPROC);
register int barno = ++(p_shm_me->barno);
register int barnonext = (barno + 1);
do {
register int hisbarno = p->barno;
if (hisbarno == barnonext) return;
if (hisbarno != barno) {
do {
P_SHM_IDLE;
hisbarno = p->barno;
if (hisbarno == barnonext) return;
} while (hisbarno != barno);
}
} while (++p < q);
}
The final optimization in the AFAPI shared memory barrier code is the insertion of P_SHM_IDLE as a suggestion to the UNIX scheduler that this job may be spin-locked for some time, and that it may therefor make sense to schedule another job. If the number of physical processors available is greater than or equal to NPROC, P_SHM_IDLE should be {} -- nothing. However, if NPROC is larger than the number of actual processors that are available, the UNIX scheduler is unaware of the fact that running this process (virtual processor) is futile until after the process that owns p->barno has incremented its counter. The ideal would be to call an operating system function that forces the scheduler to put the current process to sleep and instead runs the process whose counter is p->barno; unfortunately, there is no such function available on standard UNIX. We have found that setting P_SHM_IDLE to usleep(1) is reasonably effective in that it generally causes a minimum length sleep, giving other processes a chance to run.
For all operations that involve data, the ideal implementation would use a dedicated AFU (Aggregate Function Unit, such as TTL_PAPERS). This AFU would detect completion of a barrier, sample the data from all processors, and then compute and return the appropriate aggregate function value for each processor -- as the PAPERS hardware does. Without an AFU-like structure, data is instead transmitted using two 64-bit buffers in the same cache line as each processor's barrier counter; data associated with barrier number k goes in that processor's buffer (k & 1). Using these buffers, there are two basic approaches possible for computing the aggregate function values:
Although the second choice sounds promising, it has higher overhead due to its more complex logic and the structuring of interactions between processors also adds overhead in the form of additional synchronizations. Thus, SHMAPERS AFAPI uses the first approach.
Because the cache lines fetched to detect the barrier also hold the data, SHMAPERS AFAPI aggregates generally take only a little more time than simple barrier synchronizations.
One of the more controversial aspects of the AFAPI is the fact that the user must be aware of the actual number of processors available in the system -- NPROC. However, the SHMAPERS AFAPI does allow the user to set the value of NPROC. This feature was included, along with the P_SHM_IDLE mechanism mentioned earlier, to facilitate program development on systems with fewer processors than will be used for production runs.
The problem with virtualizing processors is that the operating system scheduler generally cannot distinguish a process/thread that is spin-waiting on a memory location from one that is doing useful work. The following graph shows the performance effect of virtual processors on barrier performance by benchmarking four different barrier implementations, with varying numbers of virtual processors, on the five-processor Sun system described earlier.
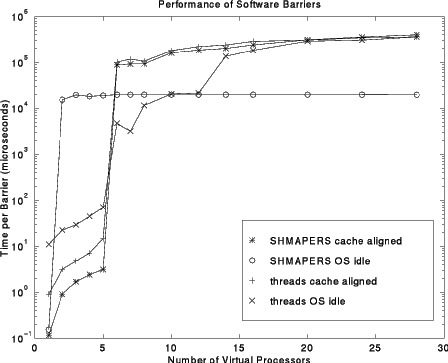
As expected, until the virtual processor count exceeds the number of physical processors, the SHMAPERS AFAPI mechanism is fastest. Between 6 and 10 virtual processors, the optimized thread-based version with thr_yield() calls performs best; this is not surprising, as thread scheduler overhead is typically less than full UNIX process scheduler overhead. However, for more than 2x the number of physical processors, SHMAPERS AFAPI with P_SHM_IDLE set to usleep(1) (a way to surrender this process timeslice) is the fastest. This approach is also remarkably stable even as the number of virtual processors becomes very large; in fact, nearly identical times were obtained using up to 28 virtual processors on a uniprocessor Pentium system. Thus, we draw two conclusions:
In earlier work, we have formulated, implemented, and shown the utility of aggregate function communication using clusters connected by various versions of the PAPERS custom hardware. We are no longer the only people using PAPERS and its library; there are now over a dozen sites outside Purdue University. The problem is that PAPERS is still not COTS -- you can't buy one off-the-shelf at the local computer store.
In this paper, we show that using COTS shared memory machines, the AFAPI which grew out of the PAPERS project is not only useful, but actually yields better performance than a cluster linked by the PAPERS hardware. Of course, shared memory systems do not scale to large systems as easily as clusters do, but it is possible to build a hybrid AFAPI that combines TTL_PAPERS AFAPI across nodes with SHMAPERS AFAPI within each node. Further, although UDPAPERS AFAPI will yield lower performance than TTL_PAPERS AFAPI, it will allow purely COTS clusters to be constructed; in a hybrid library with SHMAPERS, it could even be reasonably effective for fully COTS clusters of shared memory machines. Most importantly, all of these are/would be the same AFAPI model.
In summary, AFAPI is not just a library for accessing some strange custom hardware, but truly constitutes a third communication model with importance and efficiency on a par with that of shared memory or message passing. We suggest it is a model that offers a particularly good target for compilers, combining low latency with predictable performance.
All aspects of PAPERS and AFAPI are fully public domain, and a wide variety of projects are underway. For more information, see WWW URL:
http://garage.ecn.purdue.edu/~papers/