-
In a typical desktop PC processor, which one of the
following four memory subsystems is not found
on the processor chip?
TLB
L1 Cache
L2 Cache
Registers
All four of the above typically are on the processor chip
Registers, Write buffer, TLBs, and Caches are all typically on chip now;
main memory isn't, but even the classical NorthBridge functions have been brought
on chip with AMD's HyperTransport and Intel's QuickPath
-
Which one of the following four statements about the memory
hierarchy is false?
For comparable cache size, a direct mapped cache is easier to
build (simpler logic) than set associative cache
mostly because of replacement policy complications...
Temporal Locality refers to an object being likely to be
referenced again soon after being referenced once
Modern processors often have separate caches for instructions
and data
using caches to fake Harvard architecture makes an easier pipeline structure...
Larger cache line sizes take better advantage of Spatial
Locality
All four of the above statements are true
-
Consider the following two MIPS subset implementations:
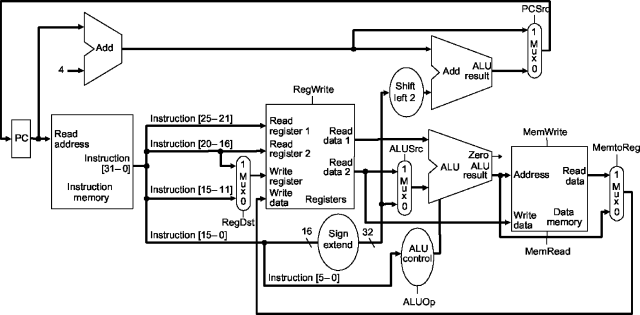
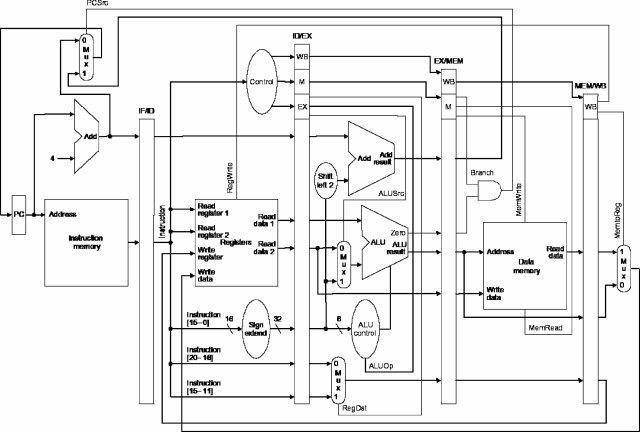
Which of the following four statements about how
pipelining changes the architecture is false?
The ALU used for operations like add and xor
could be the same circuit in both implementations
The ALU used to add 4 to the PC could be the same circuit
in both implementations
The Instruction Memory module could be the same circuit in both
implementations
The Data Memory module could be the same circuit in both
implementations
None of the above four statements is false; in fact, all of the
modules can be the same circuits in both implementations because
pipelining only adds buffers, changes/adds some datapaths, and
modifies the control logic
this is precisely why we bother with a single-cycle implementation
-
Pipelined designs generally achieve higher performance
than similar single-cycle designs by allowing a higher clock
rate, but the clock rate with a 5-stage pipeline is generally
somewhat less than 5X the speed of the single-stage design it
was derived from (e.g., compare the two MIPs implementations
given in question 5). Give one reason why the clock rate is
less than 5X.
-
The first time a modern processor executes a particular branch
instruction, it must compute the target address by adding the
offset encoded within the branch instruction to the PC value.
However, if the same instruction is executed again soon enough,
the processor does not have to recompute the target address.
Which hardware structure implements this feature?
BLT
Bacon, Lettuce, and Tomato?
TLB
Translation Lookaside Buffer -- cache for page table address translation entries
BTB
Branch Target Buffer -- cache for branch target addresses
Data Cache
Instruction Cache
close but not quite; the instruction may be in cache,
but we'd still have to fetch it, extract the offset field, and add that to the PC --
which usually takes about 1 extra clock cycle
-
Consider executing each of the following code sequences on the
pipelined MIPS implementation given below
(which does not incorporate value forwarding):

Incidentally, both code sequences produce the same final
results. Which of the following statements best describes
the execution times you would expect to observe?
(A) addi $t1,$t0,4
lw $t2,0($t0)
xor $t2,$t2,$t3 # depends on lw $t2
(B) lw $t2,0($t0)
addi $t1,$t0,4
xor $t2,$t2,$t3 # depends on lw $t2
(A) would be faster than (B)
(B) would be faster than (A)
a bigger gap between the lw and xor means a smaller bubble
(A) would take the same number of clock cycles as (B)
Which is faster depends on the values being added and xored
NO! Dependence interlocks have nothing to do with actual data values,
but are a property of the pattern in which things are referenced
-
Consider executing each of the following code sequences on the
pipelined MIPS implementation given below:

Also consider executing them on this design with value
forwarding logic and datapaths added. Which of the
following statements best describes how the forwarding
logic would alter the execution times?
(A) lw $t1,4($t0)
sw $t1,16($t2) # depends on lw $t1
beq $t1,$t3,lab # depends on lw $t1
(B) lw $t1,4($t0)
sw $t2,16($t3)
beq $t0,$t3,lab
Neither (A) nor (B) is affected by forwarding
(A) is not affected,
(B) would be faster using forwarding
(A) would be faster using forwarding,
(B) is not affected
No dependences in (B) means forwarding isn't needed -- nor does it help
Both (A) and (B) would be faster using forwarding
The execution time improvements due to forwarding depend on the
values in the registers, not on the instructions being executed;
thus, it is impossible to say how execution times for (A) and
(B) are affected
NO! Forwarding reduces pipeline bubble size associated with dependences carrying
values between instructions, so only the pattern of register references matters
-
The Intel Pentium 4 has gone through several revisions; the
following diagram shows the internals of the version known as
Prescott. According to the diagram, which of the following
techniques is not used in this design?

Branch Target Buffer
Set-associative cache
8-way means set size of 8
Separate L2 caches for code and data
I only see one L2 Cache with both instruction and data access paths
Superscalar execution of integer arithmetic
I see three ALUs in the integer portion of this design
Instruction scheduling with register renaming
The "Allocator/Register Renamer" is pretty obvious,
as are the "Scheduler uop Queues"
-
Suppose that a simple system has a single cache with an access
time of 2 clock cycles. Cache misses are satisfied with an
average memory latency of 1000 clock cycles. Assuming a cache
hit ratio of 0.9 (90%), how long does the average reference
take? Show the formula that would give the answer.
-
Given the declarations int a[N][N]; int i, j;, a C
compiler would allocate N*N words in memory for
a such that a[i][j] is (i*N)+j words
after the memory location that holds a[0][0]. Given
that N is large, which of the following two loop nests
is likely to execute faster and why:
(1) for (i=0; i<N; ++i) for (j=0; j<N; ++j) a[i][j] = 0;
(2) for (j=0; j<N; ++j) for (i=0; i<N; ++i) a[i][j] = 0;