-
For this question, mark all answers that apply.
Consider making changes to C code to speed-up execution
using a computer with a typical memory hierarchy?
(Hint: in C, a[0][0] is immediately followed by a[0][1]
in memory.)
You can speed up this:
for (int i=0; i<N; ++i) for (int j=0; j<N; ++j) a[i][j]=0;
By rewriting it as:
for (int j=0; j<N; ++j) for (int i=0; i<N; ++i) a[i][j]=0;
You can speed up this:
for (int j=0; j<N; ++j) for (int i=0; i<N; ++i) a[i][j]=0;
By rewriting it as:
for (int j=0; j<N; ++j) for (int i=0; i<N; ++i) a[j][i]=0;
Counting the number of memory references with poor locality
is probably a better predictor of performance than counting
arithmetic operations
If N is small and you do not have any relevant entries originally loaded into the TLB, you can speed up this:
struct { int a, b, c; } abc[N];
for (int i=0; i<N; ++i) { abc[i].a += abc[i].b * abc[i].c; }
By rewriting it as:
int a[N], b[N], c[N];
for (int i=0; i<N; ++i) { a[i] += b[i] * c[i]; }
You can speed up this:
struct { int a, b, c; } abc[N];
for (int i=0; i<N; ++i) { abc[i].a += abc[i].b; }
By rewriting it as:
struct { int a, b; } ab[N]; int c[N];
for (int i=0; i<N; ++i) { ab[i].a += ab[i].b; }
-
For this question, mark all answers that apply.
Which of the following statements about processor implementations are generally true?
Unsigned and signed 2's complement subtraction are really
the exact same operation at the bit level
The longest propagation delay in any stage of a pipeline
determines the fastest possible clock rate for the whole pipe
If you base the design of a pipelined processor on a
single-cycle design, then most control signals should
be set the same way to execute the same instruction
Branch prediction implies the processor will be speculatively executing some instructions,
which might need to be squashed if the prediction is wrong
Most RISC instruction sets are designed to simplify pipelined execution
of compiler-generated code
-
For this question, mark all answers that apply.
Which of the following statements about how computer equipment is evolving over time are true?
The number of processor clock cycles it takes to read a word from memory is increasing.
The Top500 supercomputers double in performance slower than transistors/chip doubles.
Moore's Law predicted an exponential increase in processor clock speed over time.
Power consumed per transistor is increasing.
Over the last decade of IEEE/ACM Supercomputing conferences, there have been
an increasing number of vendors selling plumbing supplies
-
For this question, mark all answers that apply.
Which of the following correctly describe ALU operations
as discussed in this course?
Table lookup is a viable and fast way to multiply 8-bit ints
Shift-and-add binary integer multiplication can be sped-up by using base 256 arithmetic
Speculative carry uses three half-precision adders
An integer sign extension function unit is of comparable complexity to an adder
Floating-point addition begins with denormalization to make the exponents equal
-
For this question, mark all answers that apply.
Which of the following statements your Verilog projects are true?
In the Verilog code you were given for the third team project (Assignment 5),
value forwarding is not implemented
In the Verilog code you were given for the third team project (Assignment 5),
the buffer registers between stages ID and EX have names starting with ID_
In the first team project (Assignment 1), your implementation of the mul3 instruction used the Verilog * operator
In the third team project (Assignment 5),
implementing sllv, srlv, and srav only required changes to the ID and EX stages
In the second and third team projects (Assignments 4 and 5),
the sllv, srlv, and srav instructions
are all RTYPE instructions with two source registers and one destination
-
For this question, mark all answers that apply.
Use the following MIPS pipeline diagram for answering this question.
Consider executing the following code MIPS sequence:
A: ori $t1, $t0, 275
B: slt $t3, $t2, $t1
C: addi $t4, $t0, 1250
D: sw $t4, 812($t5)
E: xor $t0, $t5, $t2
F: lw $t1, 4608($t5)
This code is to be executed on a pipelined MIPS implementation
like that shown in the reference diagram.
Unless stated otherwise, assume value forwarding is not implemented.
Which of the following statements are true?
In a machine without value forwarding,
the code would execute in less time if instruction B were moved to between C and D
As written, instruction F couldn't move to before B, but it could if we renamed
register $t1 with $t6 in instruction F
There is an anti dependence (WAR) between instructions A and B
Out-of-order execution hardware might speed-up execution of this code
Adding value forwarding to the pipeline would result in no pipeline bubbles for this code
-
For this question, mark all answers that apply.
Use the following diagram for answering this question.
Be especially careful to note the lables on the MUXes.
Given the single-cycle MIPS implementation diagram above,
and that RegDst=1, ALUSrc=1, and MemtoReg=1,
Which of the following instructions might be executing?
lw $t0, 896($t1)
and $t0, $t1, $t2
beq $t0, $t1, lab
andi $t0, $t1, 427
sw $t0, 2104($t1)
-
For this question, mark all answers that apply.
Assume any float or int is stored in 32 bits
and float arithmetic is as specified by the IEEE 754
standard for single-precision. Which of the following statements
about floating point arithmetic are true?
Floating-point reciprocal can be computed by making a guess and refining it
If all values are normal and within range, the product
of a group of floating point numbers generally produces
a more accurate result than the sum
Even if all values are normal and within range, (a*(b*c)) might not equal ((a*b)*c)
26 is precisely representable as a floating-point value
A too-large float value can be represented as infinity
-
For this question, mark all answers that apply.
Which of the following statements about computer arithmetic are true?
In IEEE 754 floating-point arithmetic, 0 is not considered a normal value.
Given float a,b,c; and that all values encountered are normal with neither overflow nor underflow,
the value of a*(b*c) is always close to that of (a*b)*c.
An 8-bit 1's complement binary integer can represent the value -127
A speculative-carry adder is better than a carry-select adder in that it uses fewer gates.
Booth's algorithm would be useful in building a circuit to multiply by 32.
-
For this question, mark all answers that apply.
Which of the following statements about Verilog code are true?
In Verilog, using parameter generally will result in a more complex hardware implementation.
Using owner computes, the owner of a register sending signals from one stage to another in a pipeline
is the stage that writes the register
Given:
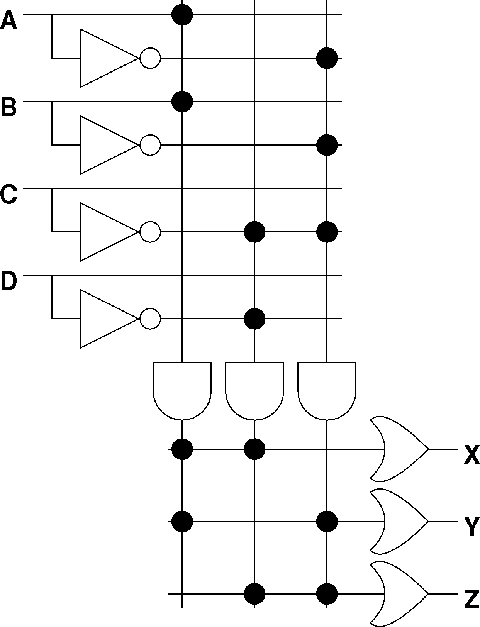
Verilog code to compute the value of wire Z; could be assign Z=((!C)&(!D))|((!A)&(!B)&(!C));
In Verilog, given wire [6:0] a,b; wire [13:0] c;, assign c={a,b}; is prefectly reasonable code
Use of recursion in Verilog is limited to non-synthesizable code
-
For this question, mark all answers that apply.
Use the following diagram for answering the next question.
The above diagram shows the internals of AMD's Zen2 processor design.
Which of the following observations about the
design are justified by the diagram?
There is some type of branch predictor
Out-of-order instruction execution (with register renaming) is used
The L1 instruction cache is direct mapped
There is a unified L2 cache for instructions and data
The L1 data cache is direct mapped
-
For this question, mark all answers that apply.
Which of the following statements about I/O are true?
Accessing a disk drive can take millions of processor clock cycles
Memory-mapped I/O operations use special instructions that cannot
be generated by C compilers, although you can use them in a C program
by calling hand-written assembly-language code
Memory-mapped I/O allows individual I/O registers to have different protection,
e.g., location 0x3bc might be writeable and 0x3bd not
DMA (Direct Memory Access) means the computer's main processor
directly moves data into I/O device registers
A typical computer monitor is now an LCD
-
For this question, mark all answers that apply.
Which of the following statements about the memory hierarchy are true?
Rather than read/write OS calls, contents of a file can be accessed using memory load/store
instructions if the file has been mapped into your virtual address space
A longer cache line size decreases misses in code with lots of temporal locality
For the same total cache capacity, a larger set size will usually decrease hit rate
The address used to search the L3 cache is usually a physical memory address
The main memory is actually treated as a cache for virtual memory on the disk,
but disk access is slow enough that a smarter replacement policy can
be implemented in software (inside the operating system) rather than hardware
-
For this question, mark all answers that apply.
Which of the following statements about performance and supercomputers are true?
A cloud really is "somebody else's computer" configured for remote
access via the internet and virtualized for sharing
Computer systems are now fast enough so that performance analysis
is no longer an issue
Communication latency is important in a parallel computer because
it effectively determines how small a grain of work can be executed
in parallel and still get speedup; with high latency, work needs to
be done in fewer, larger, chunks -- thus giving less speedup
Connecting multiple computers to each other using a switch or router
provides enough bisection bandwidth for all the connected machines
to be talking simultaneously at the full rated bandwidth
You can increase throughput by running longer jobs first
-
For this question, mark all answers that apply.
Which of the following MIPS assembly language sequences
correctly compute the integer expression value given?
To compute $t0=7*$t1:
addu $t0, $t1, $t1
addu $t0, $t0, $t0
subu $t0, $t0, $t1
To compute $t0=$t1-$t2:
subu $t0, $t1, $t2
To compute $t0=14*$t1:
addu $t2, $t1, $t1
addu $t0, $t2, $t2
addu $t0, $t0, $t0
addu $t0, $t0, $t0
subu $t0, $t0, $t2
To compute $t0=$t1&($t1-1):
addiu $t0, $t1, -1
and $t0, $t0, $t1
To compute $t0=$t1-$t2:
li $t0, -1
xor $t0, $t0, $t2
addiu $t0, $t0, 1
addu $t0, $t0, $t1
Computer Organization and Design.