A BBGates Sample

BBGates is actually one of the projects in the EE599/699 Optimizing Compilers course also taught by Prof. Dietz. This compiler takes a C program and literally converts it into an optimized gate-level design. Here's an example of what it does....

Input C Code

Our sample input file, testg.c, is about as simple a test case as is interesting:

int a, b, c;

f()
{
	b = 3;
	a = 10;
	while (a > b) {
		a = a - 1;
	}
	c = a - b;
}

So, what does that generate?

Sequential Output

The sequential output is just text (in gates.seq) that looks like:

0	lab(0)
1	const(0)
2	const(3)
3	st(b{1,1}, 2)
4	const(10)
5	st(a{1,1}, 4)
6	lab(1)
7	const(0)
8	ld(a{1,1})
9	ld(b{1,1})
10	gt(8, 9)
11	sel(10, 3, 2)
12	lab(3)
13	const(0)
14	ld(a{1,1})
15	const(1)
16	sub(14, 15)
17	st(a{1,1}, 16)
18	sel(-1, 1, 1)
19	lab(2)
20	const(0)
21	ld(a{1,1})
22	ld(b{1,1})
23	sub(21, 22)
24	st(c{1,1}, 23)
25	lab(4)

Notice that the final label is actually significant in that reaching that label is what terminates the program.

Gate-Level Textual Output

The gate-level output, generated using the -g command line option, outputs somewhat human-readable text (in gates) at the gate level:

G2 = XOR(_1, STATE_0_0_7)
G3 = XOR(_1, STATE_0_0_6)
G4 = AND(G2, G3)
G5 = XOR(_1, STATE_0_0_5)
G6 = AND(G4, G5)
G7 = XOR(_1, STATE_0_0_4)
G8 = AND(G6, G7)
G9 = XOR(_1, STATE_0_0_3)
G10 = AND(G8, G9)
G11 = XOR(_1, STATE_0_0_2)
G12 = AND(G10, G11)
G13 = XOR(_1, STATE_0_0_1)
G14 = AND(G12, G13)
G15 = XOR(_1, STATE_0_0_0)
G16 = AND(G14, G15)
G17 = XOR(_1, G16)
G18 = AND(G17, b_1_1_0)
G19 = OR(G16, G18)
G20 = AND(G17, b_1_1_1)
G21 = OR(G16, G20)
G22 = AND(G17, b_1_1_2)
G23 = AND(G17, b_1_1_3)
G24 = AND(G17, b_1_1_4)
G25 = AND(G17, b_1_1_5)
G26 = AND(G17, b_1_1_6)
G27 = AND(G17, b_1_1_7)
G28 = AND(G17, a_1_1_0)
G29 = AND(G17, a_1_1_1)
G30 = OR(G16, G29)
G31 = AND(G17, a_1_1_2)
G32 = AND(G17, a_1_1_3)
G33 = OR(G16, G32)
G34 = AND(G17, a_1_1_4)
G35 = AND(G17, a_1_1_5)
G36 = AND(G17, a_1_1_6)
G37 = AND(G17, a_1_1_7)
G38 = AND(G14, STATE_0_0_0)
G39 = XOR(_1, a_1_1_0)
G40 = XOR(_1, a_1_1_1)
G41 = XOR(_1, a_1_1_2)
G42 = XOR(_1, a_1_1_3)
G43 = XOR(_1, a_1_1_4)
G44 = XOR(_1, a_1_1_5)
G45 = XOR(_1, a_1_1_6)
G46 = XOR(_1, a_1_1_7)
G47 = XOR(G39, b_1_1_0)
G48 = AND(G39, b_1_1_0)
G49 = OR(G47, G48)
G50 = XOR(G40, b_1_1_1)
G51 = AND(G40, b_1_1_1)
G52 = AND(G49, G50)
G53 = OR(G51, G52)
G54 = XOR(G41, b_1_1_2)
G55 = AND(G41, b_1_1_2)
G56 = AND(G53, G54)
G57 = OR(G55, G56)
G58 = XOR(G42, b_1_1_3)
G59 = AND(G42, b_1_1_3)
G60 = AND(G57, G58)
G61 = OR(G59, G60)
G62 = XOR(G43, b_1_1_4)
G63 = AND(G43, b_1_1_4)
G64 = AND(G61, G62)
G65 = OR(G63, G64)
G66 = XOR(G44, b_1_1_5)
G67 = AND(G44, b_1_1_5)
G68 = AND(G65, G66)
G69 = OR(G67, G68)
G70 = XOR(G45, b_1_1_6)
G71 = AND(G45, b_1_1_6)
G72 = AND(G69, G70)
G73 = OR(G71, G72)
G74 = XOR(G46, b_1_1_7)
G75 = XOR(G73, G74)
G76 = XOR(_1, G38)
G77 = AND(G16, G76)
G78 = AND(G38, G75)
G79 = OR(G77, G78)
G80 = AND(G12, STATE_0_0_1)
G81 = AND(G80, STATE_0_0_0)
G82 = XOR(_1, _1)
G83 = XOR(_0, _1)
G84 = XOR(G82, a_1_1_0)
G85 = XOR(_1, G84)
G86 = AND(G82, a_1_1_0)
G87 = OR(G84, G86)
G88 = XOR(G83, a_1_1_1)
G89 = XOR(G87, G88)
G90 = AND(G83, a_1_1_1)
G91 = AND(G87, G88)
G92 = OR(G90, G91)
G93 = XOR(G83, a_1_1_2)
G94 = XOR(G92, G93)
G95 = AND(G83, a_1_1_2)
G96 = AND(G92, G93)
G97 = OR(G95, G96)
G98 = XOR(G83, a_1_1_3)
G99 = XOR(G97, G98)
G100 = AND(G83, a_1_1_3)
G101 = AND(G97, G98)
G102 = OR(G100, G101)
G103 = XOR(G83, a_1_1_4)
G104 = XOR(G102, G103)
G105 = AND(G83, a_1_1_4)
G106 = AND(G102, G103)
G107 = OR(G105, G106)
G108 = XOR(G83, a_1_1_5)
G109 = XOR(G107, G108)
G110 = AND(G83, a_1_1_5)
G111 = AND(G107, G108)
G112 = OR(G110, G111)
G113 = XOR(G83, a_1_1_6)
G114 = XOR(G112, G113)
G115 = AND(G83, a_1_1_6)
G116 = AND(G112, G113)
G117 = OR(G115, G116)
G118 = XOR(G83, a_1_1_7)
G119 = XOR(G117, G118)
G120 = XOR(_1, G81)
G121 = AND(G28, G120)
G122 = AND(G81, G85)
G123 = OR(G121, G122)
G124 = AND(G30, G120)
G125 = AND(G81, G89)
G126 = OR(G124, G125)
G127 = AND(G31, G120)
G128 = AND(G81, G94)
G129 = OR(G127, G128)
G130 = AND(G33, G120)
G131 = AND(G81, G99)
G132 = OR(G130, G131)
G133 = AND(G34, G120)
G134 = AND(G81, G104)
G135 = OR(G133, G134)
G136 = AND(G35, G120)
G137 = AND(G81, G109)
G138 = OR(G136, G137)
G139 = AND(G36, G120)
G140 = AND(G81, G114)
G141 = OR(G139, G140)
G142 = AND(G37, G120)
G143 = AND(G81, G119)
G144 = OR(G142, G143)
G145 = AND(G79, G120)
G146 = OR(G81, G145)
G147 = AND(G38, G120)
G148 = AND(G15, G80)
G149 = XOR(_1, b_1_1_0)
G150 = XOR(_1, b_1_1_1)
G151 = XOR(_1, b_1_1_2)
G152 = XOR(_1, b_1_1_3)
G153 = XOR(_1, b_1_1_4)
G154 = XOR(_1, b_1_1_5)
G155 = XOR(_1, b_1_1_6)
G156 = XOR(_1, b_1_1_7)
G157 = XOR(G149, a_1_1_0)
G158 = XOR(_1, G157)
G159 = AND(G149, a_1_1_0)
G160 = OR(G157, G159)
G161 = XOR(G150, a_1_1_1)
G162 = XOR(G160, G161)
G163 = AND(G150, a_1_1_1)
G164 = AND(G160, G161)
G165 = OR(G163, G164)
G166 = XOR(G151, a_1_1_2)
G167 = XOR(G165, G166)
G168 = AND(G151, a_1_1_2)
G169 = AND(G165, G166)
G170 = OR(G168, G169)
G171 = XOR(G152, a_1_1_3)
G172 = XOR(G170, G171)
G173 = AND(G152, a_1_1_3)
G174 = AND(G170, G171)
G175 = OR(G173, G174)
G176 = XOR(G153, a_1_1_4)
G177 = XOR(G175, G176)
G178 = AND(G153, a_1_1_4)
G179 = AND(G175, G176)
G180 = OR(G178, G179)
G181 = XOR(G154, a_1_1_5)
G182 = XOR(G180, G181)
G183 = AND(G154, a_1_1_5)
G184 = AND(G180, G181)
G185 = OR(G183, G184)
G186 = XOR(G155, a_1_1_6)
G187 = XOR(G185, G186)
G188 = AND(G155, a_1_1_6)
G189 = AND(G185, G186)
G190 = OR(G188, G189)
G191 = XOR(G156, a_1_1_7)
G192 = XOR(G190, G191)
G193 = XOR(_1, G148)
G194 = AND(G193, c_1_1_0)
G195 = AND(G148, G158)
G196 = OR(G194, G195)
G197 = AND(G193, c_1_1_1)
G198 = AND(G148, G162)
G199 = OR(G197, G198)
G200 = AND(G193, c_1_1_2)
G201 = AND(G148, G167)
G202 = OR(G200, G201)
G203 = AND(G193, c_1_1_3)
G204 = AND(G148, G172)
G205 = OR(G203, G204)
G206 = AND(G193, c_1_1_4)
G207 = AND(G148, G177)
G208 = OR(G206, G207)
G209 = AND(G193, c_1_1_5)
G210 = AND(G148, G182)
G211 = OR(G209, G210)
G212 = AND(G193, c_1_1_6)
G213 = AND(G148, G187)
G214 = OR(G212, G213)
G215 = AND(G193, c_1_1_7)
G216 = AND(G148, G192)
G217 = OR(G215, G216)
G218 = AND(G146, G193)
G219 = AND(G147, G193)
_a_1_1_0 = G123
_a_1_1_1 = G126
_a_1_1_2 = G129
_a_1_1_3 = G132
_a_1_1_4 = G135
_a_1_1_5 = G138
_a_1_1_6 = G141
_a_1_1_7 = G144
_b_1_1_0 = G19
_b_1_1_1 = G21
_b_1_1_2 = G22
_b_1_1_3 = G23
_b_1_1_4 = G24
_b_1_1_5 = G25
_b_1_1_6 = G26
_b_1_1_7 = G27
_c_1_1_0 = G196
_c_1_1_1 = G199
_c_1_1_2 = G202
_c_1_1_3 = G205
_c_1_1_4 = G208
_c_1_1_5 = G211
_c_1_1_6 = G214
_c_1_1_7 = G217
_STATE_0_0_0 = G218
_STATE_0_0_1 = G219
_STATE_0_0_2 = G148
_STATE_0_0_3 = _0
_STATE_0_0_4 = _0
_STATE_0_0_5 = _0
_STATE_0_0_6 = _0
_STATE_0_0_7 = _0

Notice that each line deals only with a single bit of data. Also, each bit of each variable appears as two nodes: one read at the start of the clock cycle and a second, marked with an _ prefix, which is written at the end of the clock cycle.

Gate-Level Dot Output

The textual gate-level output is difficult to understand because it is so many lines. Thus, bbgates can also generate a graphical gate-level representation. It doesn't do that directly, but creates a Graphviz description suitable for processing by Dot. Rather than looking at the Dot file (in gates.dot), here's what it looks like as a PNG graphic:

Gate-Level Verilog Output

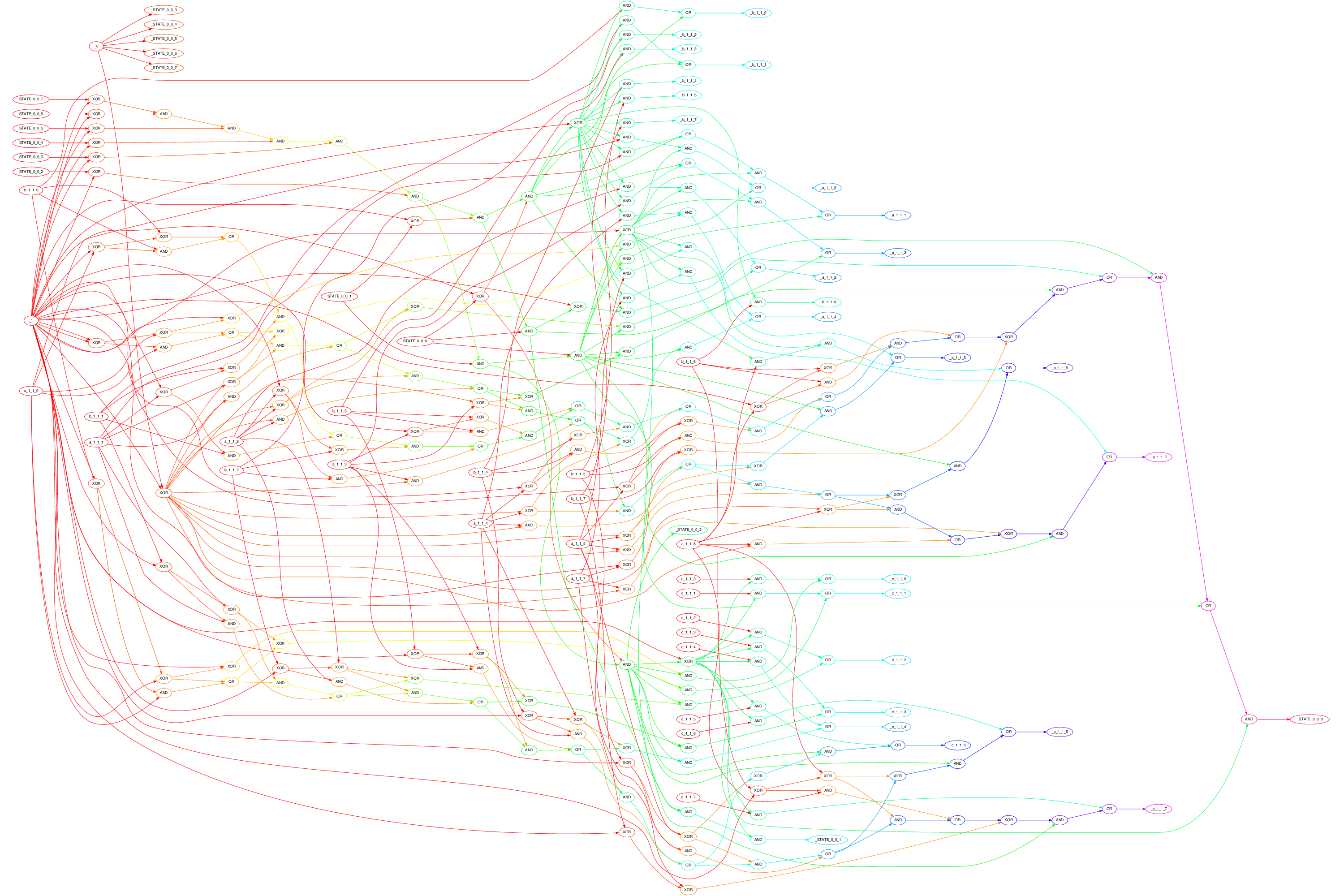
This is not quite standard Verilog code because $dumpfile is missing a file name -- but that's the only change needed to be able to run it through this HTML-form-interfaced Verilog compiler/simulator. Here's the Verilog code (in gates.v):

`define AND(A, B) (A & B) `define OR(A, B) (A | B) `define XOR(A, B) (A ^ B) `define NAND(A, B) (~(A & B)) `define NOR(A, B) (~(A | B)) module statemachine(halt, clk); output halt; input clk; reg [7:0] a_1_1; reg [7:0] b_1_1; reg [7:0] c_1_1; reg [7:0] STATE_0_0 = 0; wire [217:0] w; assign w[0] = `XOR(1, STATE_0_0[7]); assign w[1] = `XOR(1, STATE_0_0[6]); assign w[2] = `AND(w[0], w[1]); assign w[3] = `XOR(1, STATE_0_0[5]); assign w[4] = `AND(w[2], w[3]); assign w[5] = `XOR(1, STATE_0_0[4]); assign w[6] = `AND(w[4], w[5]); assign w[7] = `XOR(1, STATE_0_0[3]); assign w[8] = `AND(w[6], w[7]); assign w[9] = `XOR(1, STATE_0_0[2]); assign w[10] = `AND(w[8], w[9]); assign w[11] = `XOR(1, STATE_0_0[1]); assign w[12] = `AND(w[10], w[11]); assign w[13] = `XOR(1, STATE_0_0[0]); assign w[14] = `AND(w[12], w[13]); assign w[15] = `XOR(1, w[14]); assign w[16] = `AND(w[15], b_1_1[0]); assign w[17] = `OR(w[14], w[16]); assign w[18] = `AND(w[15], b_1_1[1]); assign w[19] = `OR(w[14], w[18]); assign w[20] = `AND(w[15], b_1_1[2]); assign w[21] = `AND(w[15], b_1_1[3]); assign w[22] = `AND(w[15], b_1_1[4]); assign w[23] = `AND(w[15], b_1_1[5]); assign w[24] = `AND(w[15], b_1_1[6]); assign w[25] = `AND(w[15], b_1_1[7]); assign w[26] = `AND(w[15], a_1_1[0]); assign w[27] = `AND(w[15], a_1_1[1]); assign w[28] = `OR(w[14], w[27]); assign w[29] = `AND(w[15], a_1_1[2]); assign w[30] = `AND(w[15], a_1_1[3]); assign w[31] = `OR(w[14], w[30]); assign w[32] = `AND(w[15], a_1_1[4]); assign w[33] = `AND(w[15], a_1_1[5]); assign w[34] = `AND(w[15], a_1_1[6]); assign w[35] = `AND(w[15], a_1_1[7]); assign w[36] = `AND(w[12], STATE_0_0[0]); assign w[37] = `XOR(1, a_1_1[0]); assign w[38] = `XOR(1, a_1_1[1]); assign w[39] = `XOR(1, a_1_1[2]); assign w[40] = `XOR(1, a_1_1[3]); assign w[41] = `XOR(1, a_1_1[4]); assign w[42] = `XOR(1, a_1_1[5]); assign w[43] = `XOR(1, a_1_1[6]); assign w[44] = `XOR(1, a_1_1[7]); assign w[45] = `XOR(w[37], b_1_1[0]); assign w[46] = `AND(w[37], b_1_1[0]); assign w[47] = `OR(w[45], w[46]); assign w[48] = `XOR(w[38], b_1_1[1]); assign w[49] = `AND(w[38], b_1_1[1]); assign w[50] = `AND(w[47], w[48]); assign w[51] = `OR(w[49], w[50]); assign w[52] = `XOR(w[39], b_1_1[2]); assign w[53] = `AND(w[39], b_1_1[2]); assign w[54] = `AND(w[51], w[52]); assign w[55] = `OR(w[53], w[54]); assign w[56] = `XOR(w[40], b_1_1[3]); assign w[57] = `AND(w[40], b_1_1[3]); assign w[58] = `AND(w[55], w[56]); assign w[59] = `OR(w[57], w[58]); assign w[60] = `XOR(w[41], b_1_1[4]); assign w[61] = `AND(w[41], b_1_1[4]); assign w[62] = `AND(w[59], w[60]); assign w[63] = `OR(w[61], w[62]); assign w[64] = `XOR(w[42], b_1_1[5]); assign w[65] = `AND(w[42], b_1_1[5]); assign w[66] = `AND(w[63], w[64]); assign w[67] = `OR(w[65], w[66]); assign w[68] = `XOR(w[43], b_1_1[6]); assign w[69] = `AND(w[43], b_1_1[6]); assign w[70] = `AND(w[67], w[68]); assign w[71] = `OR(w[69], w[70]); assign w[72] = `XOR(w[44], b_1_1[7]); assign w[73] = `XOR(w[71], w[72]); assign w[74] = `XOR(1, w[36]); assign w[75] = `AND(w[14], w[74]); assign w[76] = `AND(w[36], w[73]); assign w[77] = `OR(w[75], w[76]); assign w[78] = `AND(w[10], STATE_0_0[1]); assign w[79] = `AND(w[78], STATE_0_0[0]); assign w[80] = `XOR(1, 1); assign w[81] = `XOR(0, 1); assign w[82] = `XOR(w[80], a_1_1[0]); assign w[83] = `XOR(1, w[82]); assign w[84] = `AND(w[80], a_1_1[0]); assign w[85] = `OR(w[82], w[84]); assign w[86] = `XOR(w[81], a_1_1[1]); assign w[87] = `XOR(w[85], w[86]); assign w[88] = `AND(w[81], a_1_1[1]); assign w[89] = `AND(w[85], w[86]); assign w[90] = `OR(w[88], w[89]); assign w[91] = `XOR(w[81], a_1_1[2]); assign w[92] = `XOR(w[90], w[91]); assign w[93] = `AND(w[81], a_1_1[2]); assign w[94] = `AND(w[90], w[91]); assign w[95] = `OR(w[93], w[94]); assign w[96] = `XOR(w[81], a_1_1[3]); assign w[97] = `XOR(w[95], w[96]); assign w[98] = `AND(w[81], a_1_1[3]); assign w[99] = `AND(w[95], w[96]); assign w[100] = `OR(w[98], w[99]); assign w[101] = `XOR(w[81], a_1_1[4]); assign w[102] = `XOR(w[100], w[101]); assign w[103] = `AND(w[81], a_1_1[4]); assign w[104] = `AND(w[100], w[101]); assign w[105] = `OR(w[103], w[104]); assign w[106] = `XOR(w[81], a_1_1[5]); assign w[107] = `XOR(w[105], w[106]); assign w[108] = `AND(w[81], a_1_1[5]); assign w[109] = `AND(w[105], w[106]); assign w[110] = `OR(w[108], w[109]); assign w[111] = `XOR(w[81], a_1_1[6]); assign w[112] = `XOR(w[110], w[111]); assign w[113] = `AND(w[81], a_1_1[6]); assign w[114] = `AND(w[110], w[111]); assign w[115] = `OR(w[113], w[114]); assign w[116] = `XOR(w[81], a_1_1[7]); assign w[117] = `XOR(w[115], w[116]); assign w[118] = `XOR(1, w[79]); assign w[119] = `AND(w[26], w[118]); assign w[120] = `AND(w[79], w[83]); assign w[121] = `OR(w[119], w[120]); assign w[122] = `AND(w[28], w[118]); assign w[123] = `AND(w[79], w[87]); assign w[124] = `OR(w[122], w[123]); assign w[125] = `AND(w[29], w[118]); assign w[126] = `AND(w[79], w[92]); assign w[127] = `OR(w[125], w[126]); assign w[128] = `AND(w[31], w[118]); assign w[129] = `AND(w[79], w[97]); assign w[130] = `OR(w[128], w[129]); assign w[131] = `AND(w[32], w[118]); assign w[132] = `AND(w[79], w[102]); assign w[133] = `OR(w[131], w[132]); assign w[134] = `AND(w[33], w[118]); assign w[135] = `AND(w[79], w[107]); assign w[136] = `OR(w[134], w[135]); assign w[137] = `AND(w[34], w[118]); assign w[138] = `AND(w[79], w[112]); assign w[139] = `OR(w[137], w[138]); assign w[140] = `AND(w[35], w[118]); assign w[141] = `AND(w[79], w[117]); assign w[142] = `OR(w[140], w[141]); assign w[143] = `AND(w[77], w[118]); assign w[144] = `OR(w[79], w[143]); assign w[145] = `AND(w[36], w[118]); assign w[146] = `AND(w[13], w[78]); assign w[147] = `XOR(1, b_1_1[0]); assign w[148] = `XOR(1, b_1_1[1]); assign w[149] = `XOR(1, b_1_1[2]); assign w[150] = `XOR(1, b_1_1[3]); assign w[151] = `XOR(1, b_1_1[4]); assign w[152] = `XOR(1, b_1_1[5]); assign w[153] = `XOR(1, b_1_1[6]); assign w[154] = `XOR(1, b_1_1[7]); assign w[155] = `XOR(w[147], a_1_1[0]); assign w[156] = `XOR(1, w[155]); assign w[157] = `AND(w[147], a_1_1[0]); assign w[158] = `OR(w[155], w[157]); assign w[159] = `XOR(w[148], a_1_1[1]); assign w[160] = `XOR(w[158], w[159]); assign w[161] = `AND(w[148], a_1_1[1]); assign w[162] = `AND(w[158], w[159]); assign w[163] = `OR(w[161], w[162]); assign w[164] = `XOR(w[149], a_1_1[2]); assign w[165] = `XOR(w[163], w[164]); assign w[166] = `AND(w[149], a_1_1[2]); assign w[167] = `AND(w[163], w[164]); assign w[168] = `OR(w[166], w[167]); assign w[169] = `XOR(w[150], a_1_1[3]); assign w[170] = `XOR(w[168], w[169]); assign w[171] = `AND(w[150], a_1_1[3]); assign w[172] = `AND(w[168], w[169]); assign w[173] = `OR(w[171], w[172]); assign w[174] = `XOR(w[151], a_1_1[4]); assign w[175] = `XOR(w[173], w[174]); assign w[176] = `AND(w[151], a_1_1[4]); assign w[177] = `AND(w[173], w[174]); assign w[178] = `OR(w[176], w[177]); assign w[179] = `XOR(w[152], a_1_1[5]); assign w[180] = `XOR(w[178], w[179]); assign w[181] = `AND(w[152], a_1_1[5]); assign w[182] = `AND(w[178], w[179]); assign w[183] = `OR(w[181], w[182]); assign w[184] = `XOR(w[153], a_1_1[6]); assign w[185] = `XOR(w[183], w[184]); assign w[186] = `AND(w[153], a_1_1[6]); assign w[187] = `AND(w[183], w[184]); assign w[188] = `OR(w[186], w[187]); assign w[189] = `XOR(w[154], a_1_1[7]); assign w[190] = `XOR(w[188], w[189]); assign w[191] = `XOR(1, w[146]); assign w[192] = `AND(w[191], c_1_1[0]); assign w[193] = `AND(w[146], w[156]); assign w[194] = `OR(w[192], w[193]); assign w[195] = `AND(w[191], c_1_1[1]); assign w[196] = `AND(w[146], w[160]); assign w[197] = `OR(w[195], w[196]); assign w[198] = `AND(w[191], c_1_1[2]); assign w[199] = `AND(w[146], w[165]); assign w[200] = `OR(w[198], w[199]); assign w[201] = `AND(w[191], c_1_1[3]); assign w[202] = `AND(w[146], w[170]); assign w[203] = `OR(w[201], w[202]); assign w[204] = `AND(w[191], c_1_1[4]); assign w[205] = `AND(w[146], w[175]); assign w[206] = `OR(w[204], w[205]); assign w[207] = `AND(w[191], c_1_1[5]); assign w[208] = `AND(w[146], w[180]); assign w[209] = `OR(w[207], w[208]); assign w[210] = `AND(w[191], c_1_1[6]); assign w[211] = `AND(w[146], w[185]); assign w[212] = `OR(w[210], w[211]); assign w[213] = `AND(w[191], c_1_1[7]); assign w[214] = `AND(w[146], w[190]); assign w[215] = `OR(w[213], w[214]); assign w[216] = `AND(w[144], w[191]); assign w[217] = `AND(w[145], w[191]); assign halt = (STATE_0_0 == 4); always @(posedge clk) if (!halt) begin a_1_1[0] <= w[121]; a_1_1[1] <= w[124]; a_1_1[2] <= w[127]; a_1_1[3] <= w[130]; a_1_1[4] <= w[133]; a_1_1[5] <= w[136]; a_1_1[6] <= w[139]; a_1_1[7] <= w[142]; b_1_1[0] <= w[17]; b_1_1[1] <= w[19]; b_1_1[2] <= w[20]; b_1_1[3] <= w[21]; b_1_1[4] <= w[22]; b_1_1[5] <= w[23]; b_1_1[6] <= w[24]; b_1_1[7] <= w[25]; c_1_1[0] <= w[194]; c_1_1[1] <= w[197]; c_1_1[2] <= w[200]; c_1_1[3] <= w[203]; c_1_1[4] <= w[206]; c_1_1[5] <= w[209]; c_1_1[6] <= w[212]; c_1_1[7] <= w[215]; STATE_0_0[0] <= w[216]; STATE_0_0[1] <= w[217]; STATE_0_0[2] <= w[146]; STATE_0_0[3] <= 0; STATE_0_0[4] <= 0; STATE_0_0[5] <= 0; STATE_0_0[6] <= 0; STATE_0_0[7] <= 0; end endmodule module testbench; wire halt; reg clk = 0; statemachine m(halt, clk); initial begin $dumpfile; $dumpvars(1, m.a_1_1, m.b_1_1, m.c_1_1, m.STATE_0_0); while (!halt) begin #1 clk <= !clk; end $finish; end endmodule

Trace Output

Notice the sneaky use of `define, which you should appreciate because it makes NAND and NOR gates take an identical representation. In any case, running that through the Verilog simulator generates a pretty big HTML response, which includes:

Trace Browser For VCD Generated By vvp Simulation

   $time     a_1_1    b_1_1    c_1_1 STATE_0_0
       0: xxxxxxxx xxxxxxxx xxxxxxxx  00000000
       1: 00001010 00000011 xxxxxxxx  00000001
       3: 00001010 00000011 xxxxxxxx  00000011
       5: 00001001 00000011 xxxxxxxx  00000001
       7: 00001001 00000011 xxxxxxxx  00000011
       9: 00001000 00000011 xxxxxxxx  00000001
      11: 00001000 00000011 xxxxxxxx  00000011
      13: 00000111 00000011 xxxxxxxx  00000001
      15: 00000111 00000011 xxxxxxxx  00000011
      17: 00000110 00000011 xxxxxxxx  00000001
      19: 00000110 00000011 xxxxxxxx  00000011
      21: 00000101 00000011 xxxxxxxx  00000001
      23: 00000101 00000011 xxxxxxxx  00000011
      25: 00000100 00000011 xxxxxxxx  00000001
      27: 00000100 00000011 xxxxxxxx  00000011
      29: 00000011 00000011 xxxxxxxx  00000001
      31: 00000011 00000011 xxxxxxxx  00000010
      33: 00000011 00000011 00000000  00000100

That's pretty self-explanatory, except for the $time. It takes two simulator time units per clock cycle, one up and one down, with the state machine triggered on positive edges... which is why updates happen only on odd simulation time units.

The C program that generated this page was written by Hank Dietz using the CGIC library to implement the CGI interface.

Advanced Computer Architecture.